This article is written with much help by David Blei. It is extracted from a discussion paper on “Fast Approximate Inference for Arbitrarily Large Semiparametric Regression Models via Message Passing”. [link]

We commend Wand (2016) for an excellent description of message passing (mp) and for developing it to infer large semiparametric regression models. We agree with the author in fully embracing the modular nature of message passing, where one can define “fragments” that enable us to compose localized algorithms. We believe this perspective can aid in the development of new algorithms for automated inference.

Automated inference. The promise of automated algorithms is that modeling and inference can be separated. A user can construct large, complicated models in accordance with the assumptions he or she is willing to make about their data. Then the user can use generic inference algorithms as a computational backend in a “probabilistic programming language,” i.e., a language for specifying generative probability models.

With probabilistic programming, the user no longer has to write their own algorithms, which may require tedious model-specific derivations and implementations. In the same spirit, the user no longer has to bottleneck their modeling choices in order to fit the requirements of an existing model-specific algorithm. Automated inference enables probabilistic programming systems, such as Stan (Carpenter et al., 2016), through methods like automatic differentiation variational inference (advi) (Kucukelbir, Tran, Ranganath, Gelman, & Blei, 2016) and no U-turn sampler (nuts) (Hoffman & Gelman, 2014).

Though they aim to apply to a large class of models, automated inference algorithms typically need to incorporate modeling structure in order to remain practical. For example, Stan assumes that one can at least take gradients of a model’s joint density. (Contrast this with other languages which assume one can only sample from the model.) However, more structure is often necessary: advi and nuts are not fast enough by themselves to infer very large models, such as hierarchical models with many groups.

We believe mp and Wand’s work could offer fruitful avenues for expanding the frontiers of automated inference. From our perspective, a core principle underlying mp is to leverage structure when it is available—in particular, statistical properties in the model—which provides useful computational properties. In mp, two examples are conditional independence and conditional conjugacy.

From conditional independence to distributed computation. As Wand (2016) indicates, a crucial advantage of message passing is that it modularizes inference; the computation can be performed separately over conditionally independent posterior factors. By definition, conditional independence separates a posterior factor from the rest of the model, which enables mp to define a series of iterative updates. These updates can be run asynchronously and in a distributed environment.

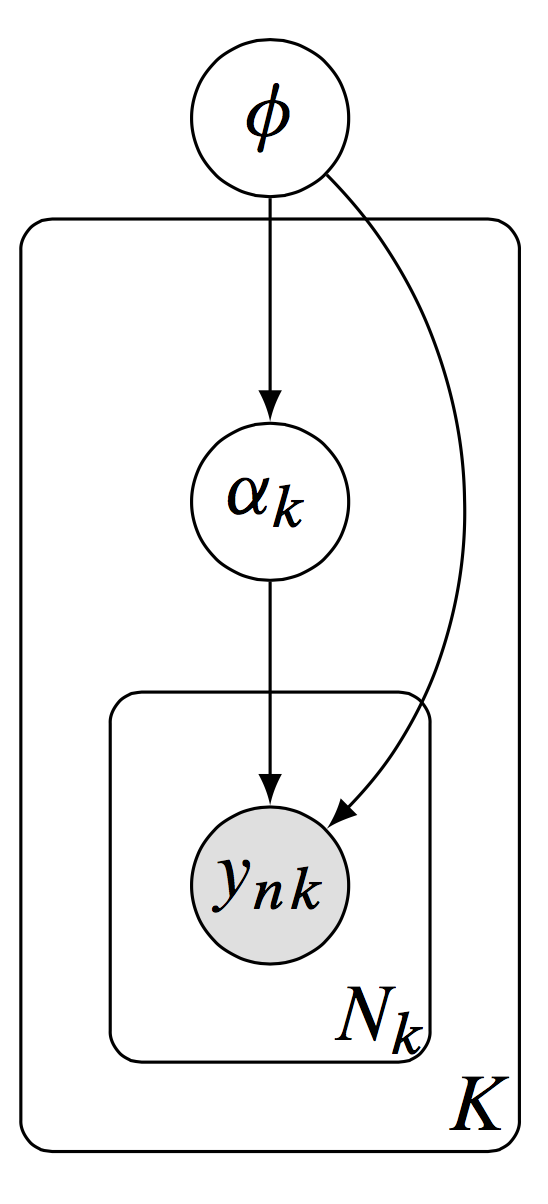
Figure 1. A hierarchical model, with latent variables $\alpha_k$ defined locally per group and latent variables $\phi$ defined globally to be shared across groups.

We are motivated by hierarchical models, which substantially benefit from this property. Formally, let $y_{nk}$ be the $n^{th}$ data point in group $k$, with a total of $N_k$ data points in group $k$ and $K$ many groups. We model the data using local latent variables $\alpha_k$ associated to a group $k$, and using global latent variables $\phi$ which are shared across groups. The model is depicted in Figure 1.

The posterior distribution of local variables $\alpha_k$ and global variables $\phi$ is

The benefit of distributed updates over the independent factors is immediate. For example, suppose the data consists of 1,000 data points per group (with 5,000 groups); we model it with 2 latent variables per group and 20 global latent variables. Passing messages, or inferential updates, in parallel provides an attractive approach to handling all 10,020 latent dimensions. (In contrast, consider a sequential algorithm that requires taking 10,019 steps for all other variables before repeating an update of the first.)

While this approach to leveraging conditional independence is straightforward from the message passing perspective, it is not necessarily immediate from other perspectives. For example, the statistics literature has only recently come to similar ideas, motivated by scaling up Markov chain Monte Carlo using divide and conquer strategies (Huang & Gelman, 2005; Wang & Dunson, 2013). These first analyze data locally over a partition of the joint density, and second aggregate the local inferences. In our work in Gelman et al. (2014), we arrive at the continuation of this idea. Like message passing, the process is iterated, so that local information propagates to global information and global information propagates to local information. In doing so, we obtain a scalable approach to Monte Carlo inference, both from a top-down view which deals with fitting statistical models to large data sets and from a bottom-up view which deals with combining information across local sources of data and models.

From conditional conjugacy to exact iterative updates. Another important element of message passing algorithms is conditional conjugacy, which lets us easily calculate the exact distribution for a posterior factor conditional on other latent variables. This enables analytically tractable messages (c.f., Equations (7)-(8) of Wand (2016)).

Consider the same hierarchical model discussed above, and set

The local factor $p(y_k,\alpha_k\mid\phi)$ has sufficient statistics $t(y_k,\alpha_k)$ and natural parameters given by the global latent variable $\phi$. The global factor $p(\phi)$ has sufficient statistics $t(\phi) = (\phi, -a(\phi))$, and with fixed hyperparameters $\eta^{(0)}$, which has two components: $\eta^{(0)} = (\eta^{(0)}_1,\eta^{(0)}_2)$.

This exponential family structure implies that, conditionally, the posterior factors are also in the same exponential families as the prior factors (Diaconis & Ylvisaker, 1979),

The global factor’s natural parameter is $\eta(\mathbf{y},\alpha) = (\eta^{(0)}_1 + \sum_{k=1}^K t(y_k, \alpha_k), \eta^{(0)}_2 + \sum_{k=1}^K N_k)$.

With this statistical property at play—namely that conjugacy gives rise to tractable conditional posterior factors—we can derive algorithms at a conditional level with exact iterative updates. This is assumed for most of the message passing of semiparametric models in Wand (2016). Importantly, this is not necessarily a limitation of the algorithm. It is a testament to leveraging model structure: without access to tractable conditional posteriors, additional approximations must be made. Wand (2016) provides an elegant way to separate out these nonconjugate pieces from the conjugate pieces.

In statistics, the most well-known example which leverages conditionally conjugate factors is the Gibbs sampling algorithm. From our own work, we apply the idea in order to access fast natural gradients in variational inference, which accounts for the information geometry of the parameter space (Hoffman, Blei, Wang, & Paisley, 2013). In other work, we demonstrate a collection of methods for gradient-based marginal optimization (Tran, Gelman, & Vehtari, 2016). Assuming forms of conjugacy in the model class arrives at the classic idea of iteratively reweighted least squares as well as the EM algorithm. Such structure in the model provides efficient algorithms—both statistically and computationally—for their automated inference.

Open Challenges and Future Directions. Message passing is a classic algorithm in the computer science literature, which is ripe with interesting ideas for statistical inference. In particular, mp enables new advancements in the realm of automated inference, where one can take advantage of statistical structure in the model. Wand (2016) makes great steps following this direction.

With that said, important open challenges still exist in order to realize this fusion.

First is about the design and implementation of probabilistic programming languages. In order to implement Wand (2016)’s message passing, the language must provide ways of identifying local structure in a probabilistic program. While that is enough to let practitioners use mp, a much larger challenge is to then automate the process of detecting local structure.

Second is about the design and implementation of inference engines. The inference must be extensible, so that users can not only employ the algorithm in Wand (2016) but easily build on top of it. Further, its infrastructure must be able to encompass a variety of algorithms, so that users can incorporate mp as one of many tools in their toolbox.

Third, we think there are innovations to be made on taking the stance of modularity to a further extreme. In principle, one can compose not only localized message passing updates but compose localized inference algorithms of any choice—whether it be exact inference, Monte Carlo, or variational methods. This modularity will enable new experimentation with inference hybrids and can bridge the gap among inference methods.

Finally, while we discuss mp in the context of automation, fully automatic algorithms are not possible. Associated to all inference are statistical and computational tradeoffs (Jordan, 2013). Thus we need algorithms along the frontier, where a user can explicitly define a computational budget and employ an algorithm achieving the best statistical properties within that budget; or conversely, define desired statistical properties and employ the fastest algorithm to achieve them. We think ideas in mp will also help in developing some of these algorithms.

References

1. Carpenter, B., Gelman, A., Hoffman, M. D., Lee, D., Goodrich, B., Betancourt, M., … Riddell, A. (2016). Stan: A probabilistic programming language. Journal of Statistical Software.
2. Diaconis, P., & Ylvisaker, D. (1979). Conjugate Priors for Exponential Families. The Annals of Statistics, 7(2), 269–281.
3. Gelman, A., Vehtari, A., Jylänki, P., Robert, C., Chopin, N., & Cunningham, J. P. (2014). Expectation propagation as a way of life. ArXiv Preprint ArXiv:1412.4869.
4. Hoffman, M. D., Blei, D. M., Wang, C., & Paisley, J. (2013). Stochastic Variational Inference. Journal of Machine Learning Research, 14, 1303–1347.
5. Hoffman, M. D., & Gelman, A. (2014). The no-U-turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo. Journal of Machine Learning Research, 15, 1593–1623.
6. Huang, Z., & Gelman, A. (2005). Sampling for Bayesian Computation with Large Datasets. SSRN Electronic Journal.
7. Jordan, M. I. (2013). On statistics, computation and scalability. Bernoulli, 19(4), 1378–1390.
8. Kucukelbir, A., Tran, D., Ranganath, R., Gelman, A., & Blei, D. M. (2016). Automatic Differentiation Variational Inference. ArXiv Preprint ArXiv:1603.00788.
9. Tran, D., Gelman, A., & Vehtari, A. (2016). Gradient-based marginal optimization. Technical Report.
10. Wand, M. P. (2016). Fast Approximate Inference for Arbitrarily Large Semiparametric Regression Models via Message Passing. ArXiv Preprint ArXiv:1602.07412.
11. Wang, X., & Dunson, D. B. (2013). Parallelizing MCMC via Weierstrass sampler. ArXiv Preprint ArXiv:1312.4605.